Énigme de finance N° 27

Question : Les actions des sociétés A et B s’échange à 50 FCFA par action aujourd’hui. Une option d’achat (un call) sur l’action A permet d’acheter 100 actions au prix de 50 FCFA par action dans un an (quelque soit le cours de l’action à ce moment). Il en est de même pour l’action B. Une option de vente (un put) sur les actions A et B permet de vendre 100 actions, respectivement, à 50 FCFA par action dans un an.

Le prix du call sur l’action A est supérieur au prix du call sur l’action B. Vu que les calls font du profit quand le prix des actions est en hausse, vous déduisez que le prix de l’action A a une plus grande chance d’évoluer à la hausse que celui de l’action B. De ce fait, vous déduisez que le prix du put sur A devrait être inférieur au put correspondant sur l’action B.

Qu’en pensez-vous ?

L’inférence est incorrecte.

En effet, la valeur du prix d’une option, qu’elle soit d’achat (call) ou de vente (put), est la somme de sa valeur intrinsèque et de sa valeur temps ou valeur spéculative. Compte tenu des caractéristiques identiques des deux titres (même prix d’exercice et cours des sous-jacents A et B), la valeur intrinsèque des options d’achat et de vente est nulle. C’est dire que si on venait à exercer les options aujourd’hui, sans attendre la maturité des options dans un an, on dégagerait un profit nul. Il vient donc nécessairement que la différence de prix entre les deux options d’achat A et B s’explique par la valeur spéculative de A qui est supérieure à celle de B. Rappelons que cette valeur est une fonction croissante de volatilité du sous-jacent et du temps jusqu’à la date d’expiration de l’option. Vu que le paramètre temps est identique, on peut déduire que la volatilité de A est le principal facteur qui explique la différence de prix. Ce facteur influence donc à la hausse à la fois la valeur du call et du put. On devra donc conclure que la plus forte volatilité du cours de l’action A induit que le prix des options d’achat et de vente écrites sur ce sous-jacent soit supérieur à celles correspondantes écrites sur le sous-jacent B.

Une seconde manière de le voir consiste à passer par la parité call-put. Compte tenu des caractéristiques identiques rappelées plus haut, on a la différence entre le prix du put et du call écrit sur A égale à celle entre le put et le call écrit sur B.

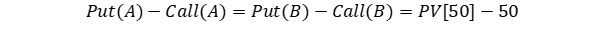
Par ailleurs vu que le prix du call (A) est supérieur au prix du call (B), on peut immédiatement conclure que le put (A) est lui aussi supérieur au prix du put (B).