Énigme de finance N° 18

Question : Soient deux obligations :

1. La première cote au pair avec un taux coupon de 1% avec une maturité de 10 ans ;
2. La seconde obligation de même maturité cote également au pair avec un taux coupon de 6%.

Si dans chacun des cas, le taux du marché augmente de 1%, laquelle des deux obligations verrait son prix varier le plus fortement ?

Pour bien traiter cette question, il faut se souvenir que la sensibilité du prix est fonction de la duration, de manière à ce que la variation du prix soit donnée par la formule :

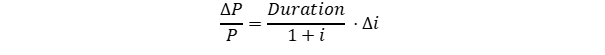
2 constatations :

• Plus le taux du coupon est faible, plus la duration est proche de la maturité car le remboursement du principal qui intervient à la maturité de l’obligation, constitue l’essentiel des flux de trésorerie que l’obligation génère. Pour s’en convaincre, pensons à une obligation zéro-coupon dont la duration est égale à la maturité. Il vient donc que l’obligation au coupon de 1% aura une duration plus élevée que celle au coupon de 6% ;

• Les obligations cotant chacune au pair, le taux actuariel du marché correspond au taux du coupon. De plus et c’est ici notre point, le facteur d’actualisation (1/1+i)  est d’autant plus élevé que le taux du marché est proche de 0. Ainsi, plus le taux actuariel de marché est faible (élevé), plus (moins) l’impact de la duration sur la variation du prix est atténué, si on peut s’exprimer ainsi.

Ces deux facteurs mis côte à côte, on peut dire que le prix de l’obligation au taux coupon de 1% baissera plus fortement que celui de l’obligation au taux coupon de 6%. Le calcul nous permet de vérifier notre raisonnement. Pour une hausse de 1% du taux actuariel de marché, l’obligation à 1% baisse de 9%, tandis que celle à 6% baisse de 7%.